16. 도박과 확률 사이
도박, 대통령선거, 그리고 확률
나의 전공은 확률론(확률모델이 보다 정확한 표현이고, 영어로는 Stochastic Model)이다. 요즘은 그냥 아무거나 하는 사람인지라, 전공에 대해서 이야기 할 일이 거의 없지만, 한창 확률 공부를 할때는 전공을 밝힐 때가 종종 있었다. 내 전공을 밝혔을 때 보통 돌아오는 말은, 도박 잘해요? 내지는 도박 잘 하겠군요. 이다. 물론, 내가 도박을 못하는건 아니지만 (물론, 그렇다고 내가 타짜라는 이야기는 더더욱 아니다), 이런 질문을 받으면, 뭐랄까.. 처음 드는 생각은
도대체 도박과 확률이 무슨 관계가 있길래?
이다. 주위에 통계를 전공한 분들도 몇분 계신데, 이런 분들도 비슷한 질문들을 받는다고 한다. 요즘은 빅데이터 내지는 비지니스 분석(Business Analtics)을 전공하는 이들에게도 비슷한 질문들을 한다고 한다. 세월이 지나 선호하는 명칭이 달라지기는 했지만, 확률이나 통계를 다루는 이들이 받는 질문들은 비슷하리라. 오늘은 도박 내지는 내기와 관련된, 그리고 확률과 통계와 관련 이야기를 해볼까 한다.
1. 이길 확률과 이긴다 것
2년 전즈음으로 기억하는데, Goolge IO Keynote에서 Google Analytics를 설명하면서, 월드컵 축구 경기의 승패를 예측한 적이 있었다. 비단, 이 때뿐이 아니다. 많은 사람들이 운동경기에 대한 이야기를 할 때는, A팀이 B팀을 이길 확률은 70% (혹은 90%) 입니다. 혹은,
A팀이 B팀을 70%의 확률로 이깁니다.
와 같은 이야기를 한다. 그런데, 가만히 생각해보라. 모든 경기의 승부의 상태는 이기거나, 지거나 (무승부가 될 경우 승부가 날 때까지 진행한다는 전제 하에) 하는 두 가지 경우밖에 없다. 즉, "70%(혹은 90%) 확률로 이긴다"와 같은 상태는 존재하지 않는다. 어떤 이벤트(혹은 상황)이 지나가고 나면, 확률이라는 것은 더 이상 소용이 없어진다. 즉, 70% 확률로 이긴다는 것은 이벤트가 끝나기전까지만 유효한 것이지, 상황이 종료되고 나면,
확률이라는 것 자체가 의미가 없어진다.
확률을 이해하는데 있어서 중요한 것은 확률에는 동시성이 존재한다는 점이다. 70%의 이길 확률이라는 것은 30%의 질 확률(이기지 않을 확률)을 의미한다. 수학적으로 표현하자면,
존재("이길 확률") == 존재("질 확률")
임을 의미 한다. 이미 결정 된 상태에 있어서는 확률이라는 숫자는 중요하지가 않다. 즉,
"이길확률"!= "이긴상태"
라는 말이다. 이게 무슨 귀신 씨나락 까먹는 소리냐고 하겠지만, 이런 귀신 씨나락 까먹는 소리를 확률은 한다.
그 귀신 씨나락 까먹는 소리를 야는 해요!! (출처: 웃찾사)이게 철학적으로는 엄청난 파장을 몰고 올 엄청나게 복잡한 문제일수도 있지만, 실제 생활에 적용하는데 있어서는 생각보다 간단할 수 있다. 다만, 그걸 받아들이는 사람은 이러한 상황을 용납하기가 힘들 뿐이다. 예를 들면 이런거다.
(정제 된) 통계(혹은 데이터 분석)을 통해 A팀이 축구 경기에서 이길 확률이 70%라고 하자. 그리고, 당신은 그 데이터 분석을 바탕으로 다음날 있을 게임에 도박(베팅)을 한다. 근데, 다음날 그 게임에 A팀이 졌다. 그렇다면, 데이터 분석이 잘못 된 것인가?
다시 한번 말하지만, 도박과 확률은 아무런 관련이 없다. 내일 경기에서 지건 이기건 지건, 데이터 분석으로 나온 (확률)값과는 직접적인 관계가 없다. 아무리 이길 확률이 높게 나오더라도, 내일(혹은 미래) 게임에 질수도 있다라는 사실에는 변함이 없다는 말이다. 아무리 데이터 분석을 통해 이길 확률이 90%라고 하더라도, 정작 도박(?)을 하는 자신의 입장(내가 도박에서 이길 확률)에서는 확률은 50%이다(이기거나 지거나)!!
작년 11월에 미국대통령 선거 때문에 한바탕 난리가 난적이 있었다. 보통 대선 후보들이 나오면, 여러가지는 경로를 통해 선호도 조사를 하게 되는데, 미국 대통령 선거가 드라마틱(?) 했었던 이유는 출구조사를 비롯한 대부분의 조사결과와는 다르게 드럼프가 미국 대통령에 당선이 되었기 때문이었을 것이다. 물론, 어떤 이들은 자신의 분석론을 통해 트럼프의 당선을 예상하기도 했었다. 이러한 분석들을 보면, 재미있는 현상이 발생하는데 그건 바로, 자신의 분석 방법의 타당성 여부를 예측 결과에 따라 판단 한다는 것이다. 많은 사람들, 심지어 통계나 데이터분석으로 밥벌이를 하는 이들 조차도, 예상이 맞으면, 통계/데이터 분석이 맞는 것으로, 예상이 틀리면, 분석이 틀린 것으로 단정 한다. 다시 한번 이야기하지만, 통계적 분석이나 데이터의 타당성이나 유효성 여부와 실제결과와 예측의 일치성 여부는 아무런 관련이 없다.
미 대선 이후, 정말 답답(?)한 마음에 몇자 글적인 페북 글 (출처: 페북)요즘은 대한민국 대통령 선거 때문에 말들이 많다. 여러 조사기관들이 누가 대통령이 될지를 예측하고 있다. 선거를 마치고, 대통령이 당선되고 나면 어떤 업체들은 자기네 조사 방법이 정확하다고 선전을 할 것이다.
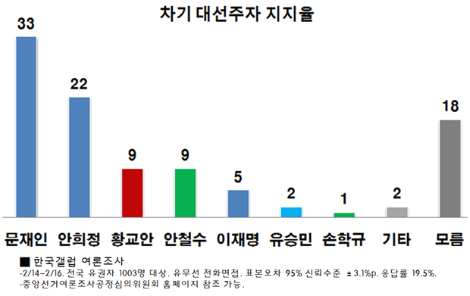2017년 2월 대선주자 지지율 (출처: 겔럽)그런데, 그들 대통령 당선자를 맞춘 것은 데이터분석 기술이 좋아서 일 가능성보다는 단순히 "운이 좋아서" 맞췄을 가능성이 훨씬 높다. 행여, 당신이 고려하고 있는 데이터 분석 회사가 자신들의 기술력의 근거로 "정확한 예측"을 제시한다면, 이런 얘들은 고려하지 않는 것이 타당하다. 왜냐하면, 이런 얘들 도박과 확률(혹은 통계)의 차이조차 모르는 얘들이니까 말이다.
2. 정작 확률이 필요할 때
그렇다면, 확률(값)이 필요한 경우는 언제 일까? 위의 축구경기 예제를 똑같이 들겠다. 다만, 조금 추가 되는 상황이 있다. 예를 들면 이런거다.
A팀 축구경기를 이길 가능성이 70%라고 한다. 당신은 내기(도박)을 할려고 하는데, 룰은 다음과 같다. 베팅을 하기 위해서는 5,000원을 내야하고, A팀이 이기면, 두배(10,000원)을 받고, 만약, A팀이 지면, 당신은 5,000원을 추가로 더 내야 한다. 당신이라면 이 내기를 참여할 것인가?
이 경우에 확률은 기대값의 형태로 의사결정을 할 수 있는 값을 제공한다. 즉, 위의 경우 기대값(Expected Value)를 구하면,
E(x) = 0.7*(5,000)+(-10,000)*0.3 = 500 (>0)
가 되며, 양의 값(+)이 되므로, 본 내기는 참여를 하는 것이 타당 하다. 확률이 도박이 아니라고 이야기 하고 있는데, 내기 이야기를 해서 좀 그런가? 그럼, 조금 다른 예를 들어 보겠다.
당신은 SW를 개발하는 회사 CEO이다. 고객으로 SW개발 일정을 당겨달라면서, 다음과 같이 제안을 해왔다. SW개발을 당겨진 일정으로 개발을 완료 해주면, 1억원의 인센티브 받고, (바뀐)일정내에 개발을 완료하지 못하면, 2억원 패널티를 내어야 한다. 현재, 당신 회사가 바뀐 일정으로 개발을 완료할수 있는 가능성은 70%라고 한다. 당신이라면, 이 제안을 받아들일 것인가?
이 문제가 좀더 현실적이라고 느껴질수도 있을 것이다. 하지만, 위의 문제는 앞에 언급했던 축구경기 내기 문제와 같은 문제이다. 확률이 도박과 다른 가장 큰 다른 점은 그 목적이
"예측"에 있는 것이 아니라 "관리"에 있다
는 점이다. 그리고, 이러한 목적은 확률을 기반으로 하는 통계, 통계를 기반으로 하는 데이터과학(혹은 빅데이터) 모두가 동일하다. 예측은 "맞는 경우"에만 관심이 있지만, 관리는 "맞는 경우"와 "맞지 않은 경우" 모두 관심을 갖는다. 그렇기에 확률을 잘한다는 의미는 (특히, 위섬성에 대한) 관리를 잘한다는 의미이지, 예측을 잘한다는 의미가 아니다.
덧붙이는 말....
1) 엄밀히 말해, 통계와 확률은 다른 학문입니다. 다만, 통계를 할때 확률에 대한 기본 지식이 있어야 하기에 확률론을 기본적으로 배우긴 합니다.
2) 저는 도박을 잘하지는 못하지만, 어디가서 크게 잃지는 않습니다....ㅎ
3) 말미에 SW개발 회사 CEO는 제안을 받아들이는 것이 타당합니다 (이유는 잘 생각해보시길...ㅋ)
